Đường tròn đường kính trực tâm trọng tâm

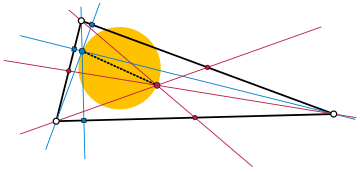
Tam giác (màu đen), trực tâm (màu xanh), trọng tâm (màu đỏ), Đường tròn đường kính trực tâm trọng tâm (màu vàng)

Trong hình học, Đường tròn đường kính trực tâm trọng tâm của một tam giác không đều là một đường tròn nhận đường kính là trọng tâm và trực tâm của tam giác.

Guinand chỉ ra rằng tâm đường tròn nội tiếp luôn nằm trong đường tròn đường kính trực tâm trọng tâm nhưng không trùng với tâm đường tròn chín điểm.[1][2][3][4] [5]:pp. 451–452

Hơn thế,[2] điểm Fermat thứ nhất, điểm Gergonne, và điểm đối trung có thể nằm trong đường tròn đường kính trực tâm trọng tâm ngoại trừ chính tâm đường tròn, trong khi điểm Fermat thứ hai luôn nằm bên ngoài đường tròn. Độ lớn của bình phương đường kính của đường tròn đường kính trực tâm trọng tâm [6]:p.102 D 2 − 4 9 ( a 2 + b 2 + c 2 ) , {\displaystyle D^{2}-{\tfrac {4}{9}}(a^{2}+b^{2}+c^{2}),} trong đó a, b, và c là độ dài cạnh của tam giác D đường kính của đường tròn ngoại tiếp tam giác đó.

Hai điểm Fermat nghịch đảo nhau qua đường tròn đường kính trực tâm trọng tâm.[7]:proposition. 3.

Trong bách khoa toàn thư về các tâm của tam giác tâm của đường tròn đường kính trọng tâm trực tâm là điểm X ( 381 ) {\displaystyle X(381)} [8]

Chú thích

  1. ^ Guinand, Andrew P. (1984), “Euler lines, tritangent centers, and their triangles”, American Mathematical Monthly, 91 (5): 290–300, JSTOR 2322671.
  2. ^ a b Bradley, Christopher J.; Smith, Geoff C. (2006), “The locations of triangle centers”, Forum Geometricorum, 6: 57–70, Bản gốc lưu trữ ngày 4 tháng 3 năm 2016, truy cập ngày 17 tháng 11 năm 2015.
  3. ^ Stern, Joseph (2007), “Euler's triangle determination problem” (PDF), Forum Geometricorum, 7: 1–9, Bản gốc (PDF) lưu trữ ngày 26 tháng 10 năm 2021, truy cập ngày 17 tháng 11 năm 2015.
  4. ^ Franzsen, William N. (2011), “The distance from the incenter to the Euler line”, Forum Geometricorum, 11: 231–236, Bản gốc lưu trữ ngày 22 tháng 10 năm 2021, truy cập ngày 17 tháng 11 năm 2015.
  5. ^ Leversha, Gerry; Smith, G. C. (tháng 11 năm 2007), “Euler and triangle geometry”, Mathematical Gazette, 91 (522): 436–452, JSTOR 40378417.
  6. ^ Altshiller-Court, Nathan, College Geometry, Dover Publications, 2007 (orig. Barnes & Noble 1952).
  7. ^ “Yiu, Paul. "The circles of Lester, Evans, Parry, and their generalizations." Forum Geometricorum 10, 175–209, 2010” (PDF). Bản gốc (PDF) lưu trữ ngày 7 tháng 10 năm 2021. Truy cập ngày 17 tháng 11 năm 2015.
  8. ^ http://faculty.evansville.edu/ck6/encyclopedia/ETC.html#X381 X(381)= MIDPOINT OF X(2) AND X(4)