Velocidade própria

Em relatividade, velocidade própria (também conhecida como celeridade) w de um objeto em relação a um observador é a razão entre o vetor deslocamento medida pelo observador ${\displaystyle {\textbf {x}}}$ e tempo próprio τ decorrido nos relógios do objeto viajante:

${\displaystyle {\textbf {w}}={\frac {d{\textbf {x}}}{d\tau }}}$

É uma alternativa à velocidade comum, a distância por unidade de tempo onde tanto a distância quanto o tempo são medidos pelo observador.

Os dois tipos de velocidade, normal e própria, são quase iguais em baixas velocidades. No entanto, em altas velocidades, a velocidade adequada retém muitas das propriedades que a velocidade perde na relatividade em comparação com teoria Newtoniana.

Por exemplo, a velocidade adequada é igual a momento por unidade de massa em qualquer velocidade e, portanto, não tem limite superior. Em altas velocidades, como mostrado na figura à direita, também é proporcional à energia de um objeto.

Velocidade própria w pode ser relacionado à velocidade ordinária v via o fator de Lorentz γ:

${\displaystyle {\textbf {w}}={\frac {d{\textbf {x}}}{dt}}{\frac {dt}{d\tau }}={\textbf {v}}\,\gamma (v)}$

onde t é tempo de coordenada ou "mapa de tempo".

Para movimento unidirecional, cada um deles também está simplesmente relacionado ao ângulo de velocidade hiperbólica de um objeto em movimento ou rapidez η por

${\displaystyle \eta =\sinh ^{-1}{\frac {w}{c}}=\tanh ^{-1}{\frac {v}{c}}=\pm \cosh ^{-1}\gamma }$.

Em espaço-tempo plano, velocidade própria é a razão entre a distância percorrida em relação a um quadro de mapa de referência (usado para definir simultaneidade) e tempo próprio τ decorrido nos relógios do objeto viajante. É igual ao momento do objeto p dividido pela sua massa de repouso m, e é composto de componentes de velocidade quadrivetor semelhantes a espaço do objeto. A monografia de William Shurcliff^[1] mencionou seu uso inicial no texto de Sears e Brehme.^[2] Fraundorf tinha explorado seu uso pedagógico^[3] enquanto Ungar,^[4] Baylis^[5] e Hestenes^[6] examinaram sua relevância das perspectivas da teoria dos grupos e da álgebra geométrica. A velocidade adequada às vezes é chamada de celeridade.^[7]

Ao contrário da mais familiar velocidade coordenada v, velocidade própria é livre de sincronia^[1] (não requer relógios sincronizados) e é útil para descrever movimentos superrelativísticos e sub-relativísticos. Assim como a velocidade coordenada e diferentemente da velocidade de quatro vetores, ela reside na fatia tridimensional do espaço-tempo definida pelo quadro do mapa. Conforme mostrado abaixo e na figura de exemplo à direita, as velocidades próprias até somam três vetores com o redimensionamento do componente fora do quadro. Isso os torna mais úteis para aplicativos baseados em mapas (e.g. engenharia) e menos úteis para obter informações sem coordenadas. Velocidade própria dividida pela velocidade da luz c é o seno hiperbólico da rapidez η, assim como o fator de Lorentz γ é o cosseno hiperbólico da rapidez e a velocidade coordenada v sobre a velocidade da luz é a tangente hiperbólica da rapidez.

Imagine um objeto viajando por uma região do espaço-tempo descrita localmente por equação métrica de espaço plano de Hermann Minkowski (cdτ)² = (cdt)² − (dx)². Aqui, um quadro de mapa de referência de parâmetros e relógios sincronizados define a posição do mapa x e mapa do tempo t respectivamente, e o d precedendo uma coordenada significa mudança infinitesimal. Um pouco de manipulação permite mostrar que a velocidade própria w = dx/dτ = γv onde, como de costume, a velocidade coordenada v = dx/dt. Assim, w finito garante que v é menor que a velocidade da luz c. Pelo agrupamento de γ com v na expressão para momento relativístico p, a velocidade própria também se estende a forma Newtoniana de momento como massa vezes velocidade para altas velocidades sem a necessidade de massa relativística.^[8]

A fórmula de adição de velocidade própria:^[9][10][4]

${\displaystyle \mathbf {u} \oplus \mathbf {v} =\mathbf {u} +\mathbf {v} +\left\{{\frac {\beta _{\mathbf {u} }}{1+\beta _{\mathbf {u} }}}{\frac {\mathbf {u} \cdot \mathbf {v} }{c^{2}}}+{\frac {1-\beta _{\mathbf {v} }}{\beta _{\mathbf {v} }}}\right\}\mathbf {u} }$

onde ${\displaystyle \beta _{\mathbf {w} }}$ é o fator beta dado por ${\displaystyle \beta _{\mathbf {w} }={\frac {1}{\sqrt {1+{\frac {|\mathbf {w} |^{2}}{c^{2}}}}}}}$.

Esta fórmula fornece um modelo de espaço girovetorial de velocidade própria de geometria hiperbólica que usa um espaço inteiro em comparação com outros modelos de geometria hiperbólica que usam discos ou semiplanos.

No caso unidirecional isso se torna comutativo e simplifica para um produto de fator de Lorentz vezes uma soma de velocidade coordenada, e.g. para w_AC = γ_ABγ_BC(v_AB + v_BC), conforme discutido na seção de aplicações abaixo.

A tabela abaixo ilustra como a velocidade adequada de w = c ou "um mapa-ano-luz por viajante-ano" é uma referência natural para a transição do movimento sub-relativístico para o super-relativístico.

Comparação de valores de referência, vários próximos da mudança de inclinação relativística em EC vs. momento.

Condição/Parâmetro	Velocidade coordenada v dx/dt em unidades de c	Velocidade angular η em i-radianos	Velocidade própria w dx/dτ em unidades de c	Fator de Lorentz γ dt/dτ = E/mc2
Viajante parado no quadro de mapa ⇔ 1 mapa-ano/viajante-ano	0	0	0	1
Momento = 12mc ⇔ 0.5 mapa-ano-luz/viajante-ano	1/√5 ≅ 0.447	ln[(1 + √5)/2] ≅ 0.481	12	√5/2 ≅ 1.118
Rapidez de 0.5 radiano hiperbólico	(e − 1)/(e + 1) ≅ 0.462	12	12(√e − 1/√e) ≅ 0.521	12(√e + 1/√e) ≅ 1.128
Velocidade coordenada = 12c ⇔ 0.5 mapa-ano-luz/mapa-ano	12	12ln[3] ≅ 0.549	1/√3 ≅ 0.577	2/√3 ≅ 1.155
Momento = mc ⇔ 1 mapa-ano-luz/viajante-ano	1/√2 ≅ 0.707	ln[1 + √2] ≅ 0.881	1	√2 ≅ 1.414
Rapidez de 1 radiano hiperbólico	(e2 − 1)/(e2 + 1) ≅ 0.761	1	12(e − 1/e) ≅ 1.175	12(e + 1/e) ≅ 1.543
Energia cinética = mc2 ⇔ 2 mapas-anos/viajante-ano	√3/2 ≅ 0.866	ln[√3 + 2] ≅ 1.317	√3 ≅ 1.732	2
Momento = 2mc ⇔ 2 mapas-anos-luz/viajante-ano	2/√5 ≅ 0.894	ln[2 + √5] ≅ 1.444	2	√5 ≅ 2.236
Rapidez de 2 radianos hiperbólicos	(e4−1)/(e4+1) ≅ 0.964	2	12(e2 − 1/e2) ≅ 3.627	12(e2 + 1/e2) ≅ 3.762
Velocidade coordenada = c ⇔ 1 mapa-ano-luz/mapa-ano	1	∞	∞	∞

Observe-se acima que a velocidade angular η e velocidade própria w varia de 0 ao infinito e seguem a velocidade coordenada quando w << c. Por outro lado, quando w >> c, velocidade própria segue o fator de Lorentz enquanto a velocidade angular é logarítmica e, portanto, aumenta muito mais lentamente.

As equações a seguir convertem entre quatro medidas alternativas de velocidade (ou velocidade unidirecional) que fluem da equação métrica do espaço plano de Minkowski:

${\displaystyle (c\delta \tau )^{2}=(c\delta t)^{2}-(\delta x)^{2}.\,}$.

${\displaystyle \gamma \equiv {\frac {dt}{d\tau }}={\sqrt {1+\left({\frac {w}{c}}\right)^{2}}}={\frac {1}{\sqrt {1-({\frac {v}{c}})^{2}}}}=\cosh(\eta )\equiv {\frac {e^{\eta }+e^{-\eta }}{2}}}$

${\displaystyle {\frac {w}{c}}\equiv {\frac {1}{c}}{\frac {dx}{d\tau }}={\frac {v}{c}}{\frac {1}{\sqrt {1-({\frac {v}{c}})^{2}}}}=\sinh(\eta )\equiv {\frac {e^{\eta }-e^{-\eta }}{2}}=\pm {\sqrt {\gamma ^{2}-1}}}$

${\displaystyle {\frac {v}{c}}\equiv {\frac {1}{c}}{\frac {dx}{dt}}={\frac {w}{c}}{\frac {1}{\sqrt {1+({\frac {w}{c}})^{2}}}}=\tanh(\eta )\equiv {\frac {e^{2\eta }-1}{e^{2\eta }+1}}=\pm {\sqrt {1-\left({\frac {1}{\gamma }}\right)^{2}}}}$

${\displaystyle \eta =\sinh ^{-1}\left({\frac {w}{c}}\right)=\tanh ^{-1}\left({\frac {v}{c}}\right)=\pm \cosh ^{-1}\left(\gamma \right)}$

ou em termos de logaritmos:

${\displaystyle \eta =\ln \left({\frac {w}{c}}+{\sqrt {\left({\frac {w}{c}}\right)^{2}+1}}\right)={\frac {1}{2}}\ln \left({\frac {1+{\frac {v}{c}}}{1-{\frac {v}{c}}}}\right)=\pm \ln \left(\gamma +{\sqrt {\gamma ^{2}-1}}\right)}$.

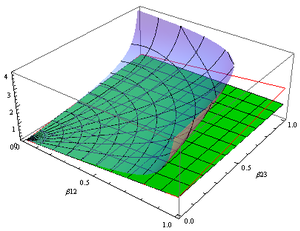
A velocidade própria é útil para comparar a velocidade dos objetos com o momento por unidade de massa em repouso (w) maior que a velocidade da luz c. A velocidade coordenada de tais objetos é geralmente próxima da velocidade da luz, enquanto a velocidade adequada indica a rapidez com que eles estão avançando nos relógios dos objetos viajantes. Isto é importante, por exemplo, se, como algumas partículas de raios cósmicos, os objetos que viajam têm uma vida útil finita. A velocidade própria também nos dá uma pista sobre o momento do objeto, que não tem limite superior.

Por exemplo, um elétron acelerado a 45 GeV pelo Grande Colisor de Elétrons e Pósitrons (LEP, de Large Electron–Positron Collider) no CERN em 1989 teria um fator de Lorentz γ de cerca de 88.000 (45 GeV dividido pela massa de repouso do elétron de 511 keV). Sua velocidade coordenada v teria sido cerca de próximo a sessenta e quatro trilionésimos da velocidade da luz c a 1 segundo-luz por segundo do mapa. Por outro lado, sua velocidade própria teria sido w = γv ~ 88.000 segundos-luz por segundo do viajante. Em comparação, a velocidade coordenada de um elétron de 250 GeV no proposto Colisor Linear Internacional (ILC de International Linear Collider)^[11] (ILC) permanecerá próximo de c, enquanto sua velocidade adequada aumentará significativamente para ~489.000 segundos-luz por segundo do viajante.

A velocidade adequada também é útil para comparar velocidades relativas ao longo de uma linha em alta velocidade. Nesse caso

${\displaystyle {\frac {p_{AC}}{m_{1}}}=w_{AC}=\gamma _{AC}v_{AC}=\gamma _{AB}\gamma _{BC}\left(v_{AB}+v_{BC}\right)=\gamma _{AB}w_{BC}+w_{AB}\gamma _{BC}\,}$

onde A, B e C referir-se a diferentes objetos ou quadros de referência.^[12] Por exemplo, w_AC refere-se à velocidade própria do objeto A em relação ao objeto C. Assim, no cálculo da velocidade relativa adequada, os fatores de Lorentz se multiplicam quando as velocidades coordenadas são somadas.

Portanto, cada um dos dois elétrons (A e C) em uma colisão frontal a 45 GeV no quadro do laboratório (B) veria o outro vindo em direção a ele a v_AC ~ c e w_AC = 88.000²(1 + 1) ~ 1.55×10¹⁰ segundos-luz por segundo do viajante. Assim, do ponto de vista do alvo, os colisores podem explorar colisões com energia de projétil e momento por unidade de massa muito maiores.

Graficando "(γ − 1) versus velocidade própria" após multiplicar o anterior por mc² e o posterior por massa m, para vários valores de m produz uma família de curvas de energia cinética versus momento que inclui a maioria dos objetos em movimento encontrados na vida cotidiana. Tais gráficos podem, por exemplo, ser usados ​​para mostrar onde a velocidade da luz, constante de Planck e energia de Boltzmann kT figuram.

Para ilustrar, a figura à direita com eixos log-log mostra objetos com a mesma energia cinética (relacionada horizontalmente) que carregam diferentes quantidades de momento, bem como como a velocidade de um objeto de baixa massa se compara (por extrapolação vertical) à velocidade após colisão perfeitamente inelástica com um objeto grande em repouso. Linhas altamente inclinadas (ascensão/curso = 2) marcam contornos de massa constante, enquanto linhas de inclinação unitária marcam contornos de velocidade constante.

Os objetos que se encaixam perfeitamente neste gráfico são humanos dirigindo carros, partículas de poeira em movimento browniano, uma nave espacial em órbita ao redor do Sol, moléculas em temperatura ambiente, um caça a jato em Mach 3, um fóton de onda de rádio, uma pessoa se movendo a um ano-luz por ano de viajante, o pulso de um [[laser] de 1,8 MegaJoule, um elétron de 250 GeV e nosso universo observável com a energia cinética do corpo negro esperada de uma única partícula a 3 Kelvin.

Aceleração própria em qualquer velocidade é a aceleração física experimentada localmente por um objeto. No espaço-tempo, é uma aceleração trivetorial em relação ao referencial de flutuação livre que varia instantaneamente do objeto.^[13] Sua magnitude α é a magnitude do quadro invariante de quadriaceleração do objeto. Aceleração própria é também é útil do ponto de vista (ou fatia do espaço-tempo) de observadores externos. Não só os observadores em todos os enquadramentos podem concordar com a sua magnitude, mas também mede até que ponto um foguete está em aceleração.

No caso unidirecional, i.e. quando a aceleração do objeto é paralela ou antiparalela à sua velocidade na fatia do espaço-tempo do observador, a mudança na velocidade adequada é a integral da aceleração adequada ao longo do tempo do mapa i.e. Δw = αΔt para a constante α. Em baixas velocidades, isso se reduz à relação bem conhecida entre a velocidade coordenada e a coordenada aceleração vezes o tempo do mapa, i.e. Δv = aΔt. Para aceleração adequada unidirecional constante, existem relações semelhantes entre rapidez η e decorrido o tempo próprio Δτ, bem como entre o fator de Lorentz γ e distância percorrida Δx. Para ser específico:

${\displaystyle \alpha ={\frac {\Delta w}{\Delta t}}=c{\frac {\Delta \eta }{\Delta \tau }}=c^{2}{\frac {\Delta \gamma }{\Delta x}}}$,

onde, como observado acima, os vários parâmetros de velocidade estão relacionados por

${\displaystyle \eta =\sinh ^{-1}\left({\frac {w}{c}}\right)=\tanh ^{-1}\left({\frac {v}{c}}\right)=\pm \cosh ^{-1}\left(\gamma \right)}$.

Estas equações descrevem algumas consequências da viagem acelerada em alta velocidade. Por exemplo, imagine uma nave espacial que possa acelerar seus passageiros a 1 g (ou 1,03 anos-luz/ano²) a meio caminho de seu destino e, em seguida, desacelerá-los em 1 g para a metade restante, de modo a fornecer gravidade artificial semelhante à da Terra a partir do ponto A ao ponto B no menor tempo possível. Para uma distância no mapa de Δx_AB, a primeira equação acima prevê um fator de Lorentz de ponto médio (acima do seu valor unitário de repouso) de γ_mid=1+α(Δx_AB/2)/c². Portanto, o tempo de ida e volta nos relógios viajantes será Δτ = 4(c/α)cosh⁻¹[γ_mid], durante o qual o tempo decorrido nos relógios dos mapas será Δt = 4(c/α)sinh[cosh⁻¹[γ_mid]].

Esta nave espacial imaginada poderia oferecer viagens de ida e volta a Proxima Centauri durando cerca de 7,1 anos do viajante (~12 anos nos relógios da Terra), viagens de ida e volta para o buraco negro central da Via Láctea de aproximadamente 40 anos (~54.000 anos decorridos nos relógios da Terra) e viagens de ida e volta a galáxia de Andrômeda com duração de cerca de 57 anos (mais de 5 milhões de anos nos relógios da Terra). Infelizmente, embora as acelerações dos foguetes de 1 g podem ser facilmente alcançados, mas não podem ser sustentados por longos períodos de tempo.^[14]

Referências

• Cinemática: para estudar as formas como a posição muda com o tempo
• Fator de Lorentz: γ = dt/dτ ou energia cinética sobre mc²
• Rapidez: ângulo de velocidade hiperbólica em radianos imaginários
• Quadrivelocidade: combinando viagens através do tempo e do espaço
• Aceleração uniforme: mantendo a aceleração coordenada fixa