粒子崩壊

粒子崩壊 (りゅうしほうかい、英: Particle decay) は、一つの素粒子が他の素粒子に変換する自発的過程 である。この過程の間、素粒子はより質量の小さい粒子とミュー粒子崩壊におけるWボソンのような媒介粒子へ変化する。次に、媒介粒子は他の粒子へと変換する。もし生成された粒子が安定でないなら、その崩壊過程は継続する。

粒子崩壊はハドロンの崩壊も言及するが、この用語は典型的には放射性崩壊を記述するのに用いられない。その二つは概念的には似ているが。放射性崩壊では、不安定原子核が粒子または放射線を放出することでより軽い原子核へと変換する。

この記事では、自然単位系、 c = ℏ = 1 {\displaystyle c=\hbar =1\,} を用いる。

粒子の生存期間と寿命の確率

粒子崩壊はポアソン過程であり、それゆえ粒子が崩壊前に生存する時間tは時定数が粒子の速度に依存する指数分布によって与えられる：

P ( t ) = e − t / ( γ τ ) {\displaystyle P(t)=e^{-t/(\gamma \tau )}\,}
ここで
τ {\displaystyle \tau } は（静止）粒子の平均寿命で、
γ = 1 1 − v 2 / c 2 {\displaystyle \gamma ={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}} は粒子のローレンツ因子である。

素粒子の寿命の表

全てのデータはParticle Data Groupによる。

型 名前 記号 エネルギー (MeV) 平均寿命
レプトン 電子 / 陽電子 e − / e + {\displaystyle e^{-}\,/\,e^{+}} 0.511 > 4.6 × 10 26   {\displaystyle >4.6\times 10^{26}\ } 年
ミュー粒子 / 反ミュー粒子 μ − / μ + {\displaystyle \mu ^{-}\,/\,\mu ^{+}} 105.6 2.2 × 10 − 6   {\displaystyle 2.2\times 10^{-6}\ } 秒
タウ粒子 / 反タウ粒子 τ − / τ + {\displaystyle \tau ^{-}\,/\,\tau ^{+}} 1777 2.9 × 10 − 13   {\displaystyle 2.9\times 10^{-13}\ } 秒
中間子 中性パイ中間子 π 0 {\displaystyle \pi ^{0}\,} 135 8.4 × 10 − 17   {\displaystyle 8.4\times 10^{-17}\ } 秒
荷電パイ中間子 π + / π − {\displaystyle \pi ^{+}\,/\,\pi ^{-}} 139.6 2.6 × 10 − 8   {\displaystyle 2.6\times 10^{-8}\ } 秒
バリオン 陽子 / 反陽子 p + / p − {\displaystyle p^{+}\,/\,p^{-}} 938.2 > 10 29   {\displaystyle >10^{29}\ } 年
中性子 / 反中性子 n / n ¯ {\displaystyle n\,/\,{\bar {n}}} 939.6 > 10 29   {\displaystyle >10^{29}\ } 年
ボース粒子 Wボソン W + / W − {\displaystyle W^{+}\,/\,W^{-}} 80,400 10 − 25   {\displaystyle 10^{-25}\ } 秒
Zボソン Z 0 {\displaystyle Z^{0}\,} 91,000 10 − 25   {\displaystyle 10^{-25}\ } 秒

崩壊率

粒子の寿命は崩壊率の Γ {\displaystyle \Gamma } 逆数で与えられる。これは単位時間あたりに粒子が崩壊する確率である。質量 M および四元運動量 P の粒子について、微分崩壊率は一般式によって与えられる：

d Γ n = S | M | 2 2 M d Φ n ( P ; p 1 , p 2 , … , p n ) {\displaystyle d\Gamma _{n}={\frac {S\left|{\mathcal {M}}\right|^{2}}{2M}}d\Phi _{n}(P;p_{1},p_{2},\dots ,p_{n})\,}
ここで
n は元の崩壊によって生成された粒子数、
S は区別できない有限状態を説明するための組み合わせ因子（以下を参照）、
M {\displaystyle {\mathcal {M}}\,} は初期状態と最終状態をつなぐ不変行列要素または確率振幅（通常はファインマンダイアグラムを用いて計算される）、
d Φ n {\displaystyle d\Phi _{n}\,} は位相空間の要素、
p i {\displaystyle p_{i}\,} は粒子 iの四元運動量である。

因子 S は次によって与えられる

S = ∏ j = 1 m 1 k j ! {\displaystyle S=\prod _{j=1}^{m}{\frac {1}{k_{j}!}}\,}
ここで
m は最終状態の区別できない粒子の集合の数、
k j {\displaystyle k_{j}\,} は 型jの粒子の数で、 ∑ j = 1 m k j = n {\displaystyle \sum _{j=1}^{m}k_{j}=n\,} である。

位相空間は次によって決定される

d Φ n ( P ; p 1 , p 2 , … , p n ) = ( 2 π ) 4 δ 4 ( P − ∑ i = 1 n p i ) ( ∏ i = 1 n d 3 p → i ( 2 π ) 3 2 E i ) {\displaystyle d\Phi _{n}(P;p_{1},p_{2},\dots ,p_{n})=(2\pi )^{4}\delta ^{4}(P-\sum _{i=1}^{n}p_{i})\left(\prod _{i=1}^{n}{\frac {d^{3}{\vec {p}}_{i}}{(2\pi )^{3}2E_{i}}}\right)\,}
ここで
δ 4 {\displaystyle \delta ^{4}\,} は四次元のディラックのデルタ関数、
p → i {\displaystyle {\vec {p}}_{i}\,} は粒子 iの（三元）運動量、
E i {\displaystyle E_{i}\,} は粒子 iのエネルギーである

規定された最終状態の全崩壊率を得るためには、位相空間に渡り積分する。

粒子が異なる最終状態への複数の崩壊分岐またはモードを持つとき、その全崩壊率は全ての分岐の崩壊率の総和を取ることによって得られる。各モードの分岐率はその崩壊率を全崩壊率で割った値で得られる。

2体崩壊

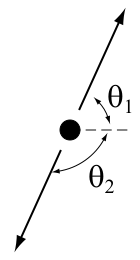運動量中心系において、一つの粒子が二つの質量が等しい粒子に崩壊する際、崩壊産物は180°の放射角度をなす。 一方、実験室系においては、崩壊粒子はおそらく光速に近い速度で運動しているので、二つの崩壊産物は運動量中心系とは異なる角度で放射される。
運動量中心系において、一つの粒子が二つの質量が等しい粒子に崩壊する際、崩壊産物は180°の放射角度をなす。
一方、実験室系においては、崩壊粒子はおそらく光速に近い速度で運動しているので、二つの崩壊産物は運動量中心系とは異なる角度で放射される。

崩壊率

質量Mの粒子が崩壊する二つの粒子を1および2とラベルする。崩壊粒子の静止系で

| p → 1 | = | p 2 → | = [ ( M 2 − ( m 1 + m 2 ) 2 ) ( M 2 − ( m 1 − m 2 ) 2 ) ] 1 / 2 2 M , {\displaystyle |{\vec {p}}_{1}|=|{\vec {p_{2}}}|={\frac {[(M^{2}-(m_{1}+m_{2})^{2})(M^{2}-(m_{1}-m_{2})^{2})]^{1/2}}{2M}},\,}

これは四元運動量がその崩壊で保存すること要求することで得られる。例えば、

( M , 0 → ) = ( E 1 , p → 1 ) + ( E 2 , p → 2 ) . {\displaystyle (M,{\vec {0}})=(E_{1},{\vec {p}}_{1})+(E_{2},{\vec {p}}_{2}).\,}

球面座標系では

d 3 p → = | p → | 2 d | p → | d ϕ d ( cos ⁡ θ ) . {\displaystyle d^{3}{\vec {p}}=|{\vec {p}}\,|^{2}\,d|{\vec {p}}\,|\,d\phi \,d\left(\cos \theta \right).\,}

デルタ関数を用いて二体の最終状態について位相空間を d 3 p → 2 {\displaystyle d^{3}{\vec {p}}_{2}} および d | p → 1 | {\displaystyle d|{\vec {p}}_{1}|\,} で積分すると、崩壊粒子の静止系での崩壊率を次のように得ることができる

d Γ = S | M | 2 32 π 2 | p → 1 | M 2 d ϕ 1 d ( cos ⁡ θ 1 ) . {\displaystyle d\Gamma ={\frac {S\left|{\mathcal {M}}\right|^{2}}{32\pi ^{2}}}{\frac {|{\vec {p}}_{1}|}{M^{2}}}\,d\phi _{1}\,d\left(\cos \theta _{1}\right).\,}

二つの異なる枠組みから

実験室系における放射粒子の角度は運動量中心系における放射粒子の角度と次の式によって関係している：

tan ⁡ θ ′ = sin ⁡ θ γ ( β / β ′ + cos ⁡ θ ) {\displaystyle \tan {\theta '}={\frac {\sin {\theta }}{\gamma \left(\beta /\beta '+\cos {\theta }\right)}}}

3体崩壊

一つの粒子が三つに崩壊する位相空間要素は次の通りである：

d Φ 3 = 1 ( 2 π ) 5 δ 4 ( P − p 1 − p 2 − p 3 ) d 3 p → 1 2 E 1 d 3 p → 2 2 E 2 d 3 p → 3 2 E 3 {\displaystyle d\Phi _{3}={\frac {1}{(2\pi )^{5}}}\delta ^{4}(P-p_{1}-p_{2}-p_{3}){\frac {d^{3}{\vec {p}}_{1}}{2E_{1}}}{\frac {d^{3}{\vec {p}}_{2}}{2E_{2}}}{\frac {d^{3}{\vec {p}}_{3}}{2E_{3}}}\,}

複素質量および崩壊率

不安定粒子の質量は形式的に複素数である。その実部は通常の意味での質量であり、虚部は自然単位系における崩壊率である。虚部が実部に比べて大きい場合、その粒子は通常、粒子と言うよりも共鳴と見なされる。これは場の量子論において質量M（実数）の粒子はよく二つの他の粒子間で交換するためである。これは、それを生成するのに十分なエネルギーがないとき、これらの他の粒子間の運動時間が1/Mのオーダーで十分に短ければ、不確定性原理に従って起こる。質量 M + i Γ {\displaystyle M+i\Gamma } の粒子にとって、粒子は1/Mの時間は運動可能だが、 1 / Γ {\displaystyle 1/\Gamma } のオーダーの時間の後に崩壊する。 Γ > M {\displaystyle \Gamma >M} ならば、粒子は通常その運動を終える前に崩壊する。

関連項目

脚注


参考文献

  • J.D. Jackson (2004). “Kinematics”. Particle Data Group. http://pdg.lbl.gov/2005/reviews/kinemarpp.pdf.  - See page 2.
  • Particle Data Group.
  • "The Particle Adventure" Particle Data Group, Lawrence Berkeley National Laboratory.