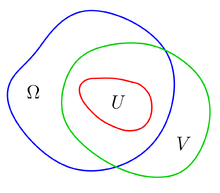
 定義で述べられている集合の図
定義で述べられている集合の図 数学の多変数複素函数の理論において、正則領域(せいそくりょういき、英: domain of holomorphy)とは、その集合よりも大きい集合に拡張出来ないような正則函数がその集合上に存在するという意味において「極大」であるような集合である。
正式に言うと、n 次元複素空間  内のある開集合
内のある開集合  が正則領域であるとは、
が正則領域であるとは、 上のすべての正則函数
上のすべての正則函数  に対して
に対して  を
を  上で満たす
上で満たす  上の正則函数
上の正則函数  が存在するような、空でない開集合
が存在するような、空でない開集合  および空でない連結開集合
および空でない連結開集合  で
で  および
および  を満たすものが存在しないことを言う。
を満たすものが存在しないことを言う。
 の場合、すべての開集合は正則領域である。すなわち、その領域の境界上の至る所で集積する零点を持つような正則函数を定義することが出来る。そのような境界はしたがって、逆函数の定義域に対する自然境界でなければならない[要出典]。
の場合、すべての開集合は正則領域である。すなわち、その領域の境界上の至る所で集積する零点を持つような正則函数を定義することが出来る。そのような境界はしたがって、逆函数の定義域に対する自然境界でなければならない[要出典]。 に対しては、ハルトークスの補題によって、上述の主張は真にはならない。
に対しては、ハルトークスの補題によって、上述の主張は真にはならない。
同値な条件
領域  に対して、以下の条件は同値である:
に対して、以下の条件は同値である:
 は正則領域
は正則領域 は正則凸
は正則凸 は擬凸
は擬凸 はレヴィ凸。すなわち、ある集合
はレヴィ凸。すなわち、ある集合  に対して
に対して  を満たすような解析的コンパクト曲面のすべての列
を満たすような解析的コンパクト曲面のすべての列  に対し、
に対し、 が成立する(
が成立する( は解析的曲面の列によって「内側から触れられる」ことはない)
は解析的曲面の列によって「内側から触れられる」ことはない) は局所レヴィ性を持つ。すなわち、すべての点
は局所レヴィ性を持つ。すなわち、すべての点  に対して、
に対して、 の近傍
の近傍  に対し、
に対し、 上の正則函数
上の正則函数  で
で  のどのような近傍にも拡張できないものが存在する。
のどのような近傍にも拡張できないものが存在する。
関係  は標準的な結果である。
は標準的な結果である。 については岡の補題を参照されたい。
については岡の補題を参照されたい。 の証明、すなわち局所的にのみ定義される拡張不可能な函数から、拡張を許さないような大域的正則函数を構成するという作業は、他のものと比べて困難である。この問題は、(エフジェニオ・エリア・レヴィ(英語版)(Eugenio Elia Levi)に因み)レヴィの問題と呼ばれ、岡潔によって初めて解かれた。その後、ラース・ヘルマンダーは函数解析と偏微分方程式の手法を使ってその問題を解いた(
の証明、すなわち局所的にのみ定義される拡張不可能な函数から、拡張を許さないような大域的正則函数を構成するという作業は、他のものと比べて困難である。この問題は、(エフジェニオ・エリア・レヴィ(英語版)(Eugenio Elia Levi)に因み)レヴィの問題と呼ばれ、岡潔によって初めて解かれた。その後、ラース・ヘルマンダーは函数解析と偏微分方程式の手法を使ってその問題を解いた( -問題の帰結である)。
-問題の帰結である)。
性質
 が正則領域であるなら、それらの共通部分
が正則領域であるなら、それらの共通部分  もまた正則領域である。
もまた正則領域である。 が正則領域の昇列であるなら、それらの合併
が正則領域の昇列であるなら、それらの合併  もまた正則領域である(ベーンケ=シュタインの定理を参照)。
もまた正則領域である(ベーンケ=シュタインの定理を参照)。- 正則領域
 の積
の積  もまた正則領域である。
もまた正則領域である。 - クザンの第一問題は正則領域において常に解くことが出来る。いくつかの位相空間論的な仮定の下では、クザンの第二問題も同様に正則領域において解くことが出来る。
関連項目
参考文献
- Steven G. Krantz. Function Theory of Several Complex Variables, AMS Chelsea Publishing, Providence, Rhode Island, 1992.
- Boris Vladimirovich Shabat, Introduction to Complex Analysis, AMS, 1992
この記事は、クリエイティブ・コモンズ・ライセンス 表示-継承 3.0 非移植のもと提供されているオンライン数学辞典『PlanetMath』の項目Domain of holomorphyの本文を含む






































