Curva del drago di Heighway

La curva del drago di Heighway, o semplicemente curva del drago ( o "Curva di Harter-Heighway" o "Drago di Heighway"), è una curva ricorsiva non auto-intersecante il cui nome deriva dalla sua somiglianza con la nota creatura mitica. Fu per la prima volta studiata dal fisico della NASA John Heighway in collaborazione con Bruce Banks e William Harter. La curva è un frattale che viene sviluppato costruendo due lati del quadrato che ha per diagonale un segmento dato, quindi il segmento iniziale viene cancellato; si ripete il processo di sostituzione sui due segmenti ottenuti alternando l'orientamento dei triangoli (non alternando l'orientamento si ottiene la curva del drago di Lévy); si ripete quest'operazione innumerevoli volte per ogni segmento risultante dall'insieme di sostituzioni precedenti.

È stata descritta da Martin Gardner nella sua Cronaca dei giochi matematici degli Stati Uniti nel 1967. Molte delle sue proprietà sono state pubblicate da Chandler Davis e Donald Knuth.

Come detto sopra questa curva può essere descritta in questo modo: partendo da un segmento di base, si sostituisca ogni segmento con due segmenti uguali uniti ad angolo retto e con una rotazione di 45° alternativamente a destra e a sinistra, si reiteri quindi l'operazione:^[1]

Può essere formalizzato come sistema di Lindenmayer con^[1]

• angolo 90°
• stringa iniziale FX
• regole di riscrittura delle stringhe
  • X ${\displaystyle \mapsto }$ X+YF+
  • Y ${\displaystyle \mapsto }$ -FX-Y

dove

• F=traccia linea,
• X/Y=posizione pari o dispari,
• +/-=+90°/-90°

La curva del drago di Heighway è più semplicemente descritta come l’insieme limite del seguente sistema di funzioni iterate nel piano complesso:

${\displaystyle f_{1}(z)={\frac {(1+i)z}{2}}}$

${\displaystyle f_{2}(z)=1-{\frac {(1-i)z}{2}}}$

con i punti iniziali nell'insieme ${\displaystyle S_{0}=\{0,1\}}$.

Utilizzando invece coppie di numeri reali, è descritta dalle due funzioni che consistono in:

${\displaystyle f_{1}(x,y)={\frac {1}{\sqrt {2}}}{\begin{pmatrix}\cos {\frac {\pi }{4}}&-\sin {\frac {\pi }{4}}\\\sin {\frac {\pi }{4}}&\cos {\frac {\pi }{4}}\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}}$

${\displaystyle f_{2}(x,y)={\frac {1}{\sqrt {2}}}{\begin{pmatrix}\cos {\frac {3}{4}}\pi &-\sin {\frac {3}{4}}\pi \\\sin {\frac {3}{4}}\pi &\cos {\frac {3}{4}}\pi \end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}+{\begin{pmatrix}1\\0\end{pmatrix}}}$

Tracciando un'iterazione della curva del drago di Heighway da un'estremità all'altra, si incontra una serie di “svolte” a 90°, alcune a destra e altre a sinistra. Per le prime iterazioni, la sequenza delle curve destra (Dª) e sinistra (Sª) è la seguente:

1ª iterazione: Dª

2ª iterazione: Dª • Dª • Sª

3ª iterazione: Dª • Dª • Sª • Dª • Dª • Sª • Sª

4ª iterazione: Dª • Dª • Sª • Sª • Dª • Sª • Sª • Dª • Dª • Dª • Sª • Sª • Dª • Sª • Sª.

Questo suggerisce il seguente schema: ogni iterazione è formata prendendo l'iterazione precedente, aggiungendo una Dª alla fine, e quindi prendendo di nuovo l'iterazione originale, ruotandola retrograda, scambiando ogni lettera e aggiungendo il risultato dopo la Dª. A causa dell'auto -similitudine mostrata dalla curva del drago, questo significa in effetti che ogni iterazione successiva aggiunge una copia dell'ultima iterazione ruotata in senso antiorario al frattale.

Questo modello a sua volta suggerisce il seguente metodo per creare modelli di iterazioni della curva di Heighway piegando una striscia di carta. Prendi una striscia di carta e piegala a metà a destra. Piegalo di nuovo a metà a destra. Se si riaprisse la striscia a questo punto la sequenza di svolte sarebbe RRL, cioè la seconda delle iterazioni sopra riportate. Continuando invece a piegare nuovamente la striscia a metà a destra, la sequenza di svolte della striscia (se venisse spiegata ora) è RRLRRLL - la terza iterazione. Continuando a piegare la striscia a metà a destra si creerebbero ulteriori iterazioni del drago di Heighway (anche se, in pratica, la striscia diventa troppo spessa per piegarsi bruscamente dopo quattro o cinque iterazioni).

Nonostante il suo aspetto complicato, la curva del drago di Heighway ha dimensioni semplici.

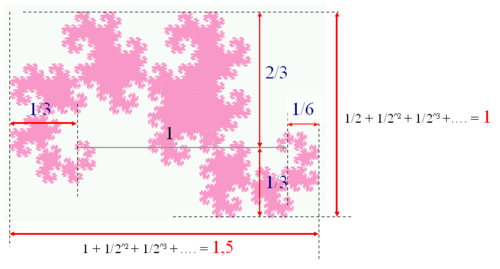
Si noti che i valori ${\displaystyle 1}$ e ${\displaystyle 1,5}$ sono limiti e non valori effettivi. Anche la sua superficie è abbastanza semplice: se il segmento iniziale è uguale a 1, la sua superficie è uguale a ${\displaystyle \textstyle {\frac {1}{2}}}$.^[3] Questo risultato è stato ricavato grazie alle sue capacità di tassellazione (vedere sotto).

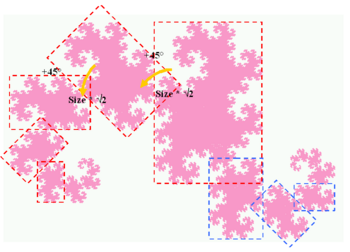
La sua dimensione frattale è ${\displaystyle \textstyle {{\frac {\ln 2}{\ln {\sqrt {2}}}}=2}}$.^[3]

E in effetti molte "auto-similitudini" possono essere viste in questa curva. La più ovvia è la ripetizione dello stesso modulo con un'inclinazione di 45° e con un rapporto di riduzione di ${\displaystyle \textstyle {\sqrt {2}}}$.

La sua frontiera (o bordo) ha una lunghezza infinita, poiché aumenta di un fattore maggiore di ${\displaystyle 1}$ a ogni iterazione, ma la sua dimensione frattale è stata approssimata numericamente da Chang e Zhang^[4][5] ${\displaystyle \log _{2}\left({\frac {1+{\sqrt[{3}]{73-6{\sqrt {87}}}}+{\sqrt[{3}]{73+6{\sqrt {87}}}}}{3}}\right)\approx 1,523627086202492.}$

Che è la radice dell'equazione:${\displaystyle \textstyle {4^{x}(2^{x}-1)=4(2^{x}+1).}}$

La curva del drago può tassellare il piano in differenti modi.

Ingrandendo si vede che vengono usati i seguenti elementi di incastro

Essa può anche tassellare se stessa

E in dimensioni crescenti forma una spirale, con 4 di queste spirali si può tassellare il piano

• Wikimedia Commons contiene immagini o altri file sulla Curva del drago di Heighway

• (EN) Eric W. Weisstein, Curva del drago di Heighway, su MathWorld, Wolfram Research.

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica