Cikkcakkszorzat

A matematika, azon belül a gráfelmélet területén a G és H gráfok cikkcakkszorzata (zig-zag product) egy gráfszorzás, olyan kétváltozós gráfművelet, amely reguláris gráfok rendezett párjaihoz egy új gráfot rendel. A ${\displaystyle G\circ H}$, eredetileg ${\displaystyle G}$ Ⓩ ${\displaystyle H}$ cikkcakkszorzat vesz egy nagyméretű (${\displaystyle G}$) és egy kisméretű (${\displaystyle H}$) reguláris gráfot, és eredményül olyan gráfot ad, ami lehetőség szerint mindkét gráf számunkra kívánatos tulajdonságait örökli: az egyik gráfban bármely két csúcs között létezik rövid út, a másik pedig állandó fokszámú. A szorzatgráf konstans fokszámú lesz, és mégis rövid úton el lehet jutni tetszőleges csúcsából egy másikba. A cikkcakkszorzat fontos tulajdonsága, hogy ha ${\displaystyle H}$ jó expander, akkor az eredménygráf expanziója alig rosszabb ${\displaystyle G}$ expanziójánál.

Nagy vonalakban a ${\displaystyle G\circ H}$ cikkcakk-gráfszorzat ${\displaystyle G}$ minden csúcsát lecseréli a ${\displaystyle H}$ egy kópiájával (felhőjével), a csúcsokat pedig úgy köti össze, hogy először egy kis lépést (cikk) tesz a felhőben, majd egy nagy lépést (cakk), majd még egy kis lépést a célfelhőben.

A cikkcakkszorzatot (Reingold, Vadhan & Wigderson 2000) vezette be. Megjelenésekor a konstans fokú expanderek és extraktorok explicit konstrukciójához használták. Később a cikkcakkszorzatot a számítási bonyolultságelméletben az SL és L bonyolultsági osztályok azonosságának bizonyítására használták fel (Reingold 2008), amiért később megkapták a Gödel-díjat.^[1]

Az alábbiakban szereplő gráfok mind irányítatlanok és regulárisak, továbbá az első gráf fokszáma megfelel a második gráf csúcsai számának.

A szerzők munkáját^[2] követve tekintsük először a cikkcakkszorzat egyszerűsített változatát. Ebben a definícióban csak olyan ${\displaystyle D}$-reguláris gráfokat tekintsünk, melyek ${\displaystyle D}$ színnel ^[3] élszínezhetők. Egy ilyen „jó” élszínezésben az ugyanabból a csúcsból kiinduló bármely két él különböző színű.

Legyen ${\displaystyle G}$ ${\displaystyle D}$-reguláris gráf ${\displaystyle N}$ csúccsal, továbbá ${\displaystyle H}$ egy ${\displaystyle d}$-reguláris gráf ${\displaystyle D}$ csúccsal. Vegyük észre, hogy ${\displaystyle D}$ megegyezik ${\displaystyle G}$ fokszámával, ${\displaystyle G}$ színeinek számával és ${\displaystyle H}$ csúcsainak számával is: ${\displaystyle H}$ csúcsait tetszőlegesen kiszínezzük ezzel a ${\displaystyle D}$ színnel.

• 
  A 4-reguláris G a bal oldalon, az 1-reguláris H a jobbon.
• 
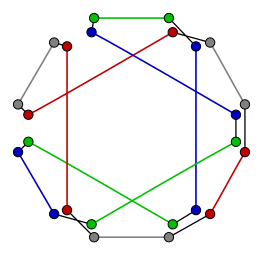  G csúcsait kicseréltük H-ból álló felhőkre.
• 
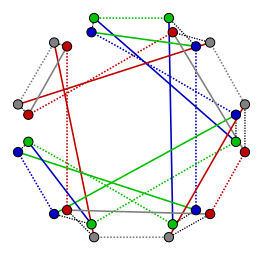  A cikkcakk-élek cseréjének művelete.
• 
  Az eredményül kapott ${\displaystyle G\circ H}$ 1-reguláris.

A következő lépésekkel nyerhető ki ${\displaystyle G}$ és ${\displaystyle H}$ cikkcakkszorzata, melyet ${\displaystyle G\circ H}$^[4]-val jelölünk:

• Cseréljük ki ${\displaystyle G}$ minden csúcsát a ${\displaystyle H}$ gráf egy-egy kópiájára, avagy „felhőjére”.
• Az eredménygráf két csúcsa, ${\displaystyle v}$ és ${\displaystyle w}$ akkor szomszédosak, hogyha létezik olyan ${\displaystyle a}$ és ${\displaystyle b}$ csúcs, melyekre:
  • ${\displaystyle v}$ és ${\displaystyle a}$ szomszédosak ${\displaystyle H}$-ban (a „cikk”-ben);
  • ${\displaystyle a}$ és ${\displaystyle b}$ azonos színűek, és ${\displaystyle G}$-ben szomszédos csúcsokból származtatott felhőkhöz tartoznak ;
  • ${\displaystyle b}$ és ${\displaystyle w}$ szomszédosak ${\displaystyle H}$-ban (a „cakk”-ban);.

Az eredménygráf:

• ${\displaystyle N\cdot D}$ csúcsot tartalmaz, hiszen a ${\displaystyle G}$ ${\displaystyle N}$ csúcsát egyenként kicseréltük a ${\displaystyle D}$ csúcsot tartalmazó ${\displaystyle H}$-kkkal;
• fokszáma ${\displaystyle d^{2}}$, hiszen adott csúcsból ${\displaystyle d}$ lehetőség van a „cikk”-re, egyetlen lehetőség a köztes lépésre majd újabb ${\displaystyle d}$ lépés a „cakk”-ra.

• 
  Ezúttal H 2-reguláris.
• 
  A csúcsok cseréje után.
• 
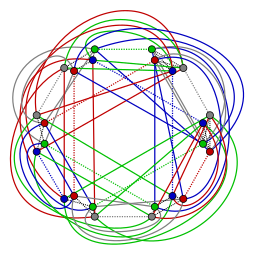  A cikkcakk.
• 
  Az eredményül kapott ${\displaystyle G\circ H}$ most 4-reguláris.

Az általános esetben nem tehető fel, hogy ismert a gráf D-élszínezése.

Számozzuk meg az egy-egy csúcsból kiinduló éleket egész számokkal, az ${\displaystyle N}$ csúcsú gráf esetében ${\displaystyle 1}$ - ${\displaystyle N}$-ig, jelöljük ezt ${\displaystyle [N]}$-nel. A ${\displaystyle (v,i)}$ rendezett pár jelölje a ${\displaystyle v}$ csúcsból kiinduló ${\displaystyle i}$-edik élt.

Feltételezve, hogy ${\displaystyle G}$ ${\displaystyle D}$-reguláris (minden csúcs fokszáma ${\displaystyle D}$), a

${\displaystyle \mathrm {Rot} _{G}:[N]\times [D]\to [N]\times [D]}$

rotáció alkalmazása a következőképp történik:

${\displaystyle \mathrm {Rot} _{G}(v,i)=(w,j),}$

amennyiben a ${\displaystyle v}$-ből kijövő ${\displaystyle i}$-edik él ${\displaystyle w}$-be vezet és a ${\displaystyle w}$-ből kijövő ${\displaystyle j}$-edik él ${\displaystyle v}$-be; tehát ha a ${\displaystyle [v,w]}$ él létezik, akkor az a ${\displaystyle v}$-ből kijövő ${\displaystyle i}$-edik él, valamint a ${\displaystyle w}$-ből kijövő ${\displaystyle j}$-edik él.

A rotáció alkalmazása helyettesíti, illetve általánosítja az előző definíció élszínezési feltételét. Ha egy D színnel történő színezés lehetséges, akkor lehetséges a csúcsok körüli éleket úgy számozni, hogy ${\displaystyle i=j}$ fennálljon.

A definícióból következik, hogy ${\displaystyle \mathrm {Rot} _{G}}$ bijekció, továbbá ${\displaystyle \mathrm {Rot} _{G}\circ \mathrm {Rot} _{G}}$ megegyezik az identitásfüggvénnyel; más szavakkal, a ${\displaystyle \mathrm {Rot} _{G}}$ egy involúció.

Legyen ${\displaystyle G}$ egy ${\displaystyle D}$-reguláris gráf az ${\displaystyle [N]}$ csúcshalmazon a ${\displaystyle \mathrm {Rot} _{G}}$ rotációs leképezéssel és legyen ${\displaystyle H}$ egy ${\displaystyle d}$-reguláris gráf a ${\displaystyle [D]}$ csúcshalmazon a ${\displaystyle \mathrm {Rot} _{H}}$ rotációs leképezéssel. A ${\displaystyle G\circ H}$ cikkcakkszorzat ekkor egy ${\displaystyle d^{2}}$-reguláris gráf az ${\displaystyle [N]\times [D]}$ csúcshalmazon, melynek rotációs térképe ${\displaystyle \mathrm {Rot} _{G\circ H}}$, méghozzá:
${\displaystyle \mathrm {Rot} _{G\circ H}((v,a),(i,j))}$:

1. Legyen ${\displaystyle (a',i')=\mathrm {Rot} _{H}(a,i)}$.
2. Legyen ${\displaystyle (w,b')=\mathrm {Rot} _{G}(v,a')}$.
3. Legyen ${\displaystyle (b,j')=\mathrm {Rot} _{H}(b',j)}$.
4. Kimenet ${\displaystyle ((w,b),(j',i'))}$.

A ${\displaystyle G\circ H}$ gráf csúcsai ${\displaystyle [N]\times [D]}$-beli ${\displaystyle (v,a)}$ párosok. A gráf élei a ${\displaystyle d}$-reguláris gráf ${\displaystyle (i,j)}$ címkéit viszik tovább, melyek az adott csúcsból kiinduló két döntésnek felelnek meg.

A definícióból következően a cikkcakkszorzat a ${\displaystyle G}$ gráfból egy új, ${\displaystyle d^{2}}$-reguláris gráfot állít elő. Tehát ha ${\displaystyle G}$ jelentősen nagyobb ${\displaystyle H}$-nál, a cikkcakkszorzat csökkenteni fogja ${\displaystyle G}$ fokszámát. Nagy vonalakban az történik, hogy a ${\displaystyle G}$ egyes csúcsait ${\displaystyle H}$ méretű felhővé amplifikálva (felerősítve), az eredeti csúcshoz tartozó élek elosztásra kerülnek a csúcsot helyettesítő felhő csúcsai között.

Egy gráf expanziója a gráf spektrális résével mérhető. A cikkcakkszorzat fontos tulajdonsága a spektrális rés megőrzése. Tehát, ha ${\displaystyle H}$ egy „elég jó” expander (nagy a spektrális rése), akkor a cikkcakkszorzat expanziója közel van ${\displaystyle G}$ eredeti expanziójához.

Formálisan: Legyen az ${\displaystyle (N,D,\lambda )}$-gráf egy ${\displaystyle N}$ csúcsú ${\displaystyle D}$-reguláris gráf, melynek (a kapcsolódó véletlen sétájának) második legnagyobb sajátértéke abszolút értékben legfeljebb ${\displaystyle \lambda }$.

Legyen ${\displaystyle G_{1}}$ egy ${\displaystyle (N_{1},D_{1},\lambda _{1})}$-gráf és ${\displaystyle G_{2}}$ egy ${\displaystyle (D_{1},D_{2},\lambda _{2})}$-gráf; ekkor ${\displaystyle G\circ H}$ egy ${\displaystyle (N_{1}\cdot D_{1},D_{2}^{2},f(\lambda _{1},\lambda _{2}))}$-gráf, ahol ${\displaystyle f(\lambda _{1},\lambda _{2})<\lambda _{1}+\lambda _{2}+\lambda _{2}^{2}}$.

A ${\displaystyle G\circ H}$ cikkcakkszorzat ${\displaystyle G}$ minden összefüggő komponensére külön hat.

Formálisan, ha adott két gráf: ${\displaystyle G}$, egy ${\displaystyle D}$-reguláris gráf ${\displaystyle [N]}$ csúcshalmazon és ${\displaystyle H}$, egy ${\displaystyle d}$-reguláris gráf a ${\displaystyle [D]}$ csúcshalmazon – akkor ha ${\displaystyle S\subseteq [N]}$ ${\displaystyle G}$ összefüggő komponense, akkor ${\displaystyle G|_{S}\circ H=G\circ H|_{S\times D}}$, ahol ${\displaystyle G|_{S}}$ a ${\displaystyle G}$ ${\displaystyle S}$ által feszített részgráfja (tehát a gráf ${\displaystyle S}$ csúcsaival, ami tartalmazza a ${\displaystyle G}$ összes olyan élét, ami ${\displaystyle S}$ csúcsai között húzódik).

2002-ben Omer Reingold, Salil Vadhan és Avi Wigderson megadtak egy egyszerű, explicit kombinatorikus konstrukciót a konstans fokszámú expander gráfok előállítására. A konstrukció iteratív, egyetlen, egyszerű építőeleme egy konstans méretű expandert használ. A cikkcakkszorzat minden iteráció során előállít egy új, megnövelt méretű, de változatlan fokszámú és expanziójú gráfot. Ezzel a módszerrel tetszőlegesen nagy expanderek létrehozhatók.

A cikkcakkszorzat fent említett tulajdonságaiból látható, hogy egy nagy gráf kis gráffal való szorzata a nagy gráf méretéhez és a kis gráf fokszámához hasonló lesz, megőrizve mindkettő expanziós tulajdonságait, így lehetővé téve az expander méretének káros mellékhatások nélküli növelését.

2005-ben Omer Reingold bemutatott egy algoritmust, ami logaritmikus térben megoldja az irányítatlan st-elérhetőségi problémát, azaz annak a problémáját, hogy egy irányítatlan gráf két csúcsa között létezik-e út. Az algoritmus erősen épít a cikkcakkszorzás műveletére.

A probléma megoldásához a bemeneti gráf hatványozás és cikkcakkszorzat kombinációjával transzformálásra kerül egy konstans fokszámú, logaritmikus átmérőjű reguláris gráffá. A hatványozás a fokszám növelésének árán növeli az expanziót (így csökkenti az átmérőt), a cikkcakkszorzat pedig csökkenti a fokszámot és megtartja az expanziót.

• Ez a szócikk részben vagy egészben a Zig-zag product című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
• Ez a szócikk részben vagy egészben a Produit zig-zag de graphes című francia Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

• Véletlen séta gráfokon, expanderek (Szabó Dániel BSC szakdolgozat)

• Reingold, O.; Vadhan, S. & Wigderson, A. (2000), "Entropy waves, the zig-zag graph product, and new constant-degree expanders and extractors", Proc. 41st IEEE Symposium on Foundations of Computer Science (FOCS), pp. 3–13, DOI 10.1109/SFCS.2000.892006.
• Reingold, O (2008), "Undirected connectivity in log-space", Journal of the ACM 55 (4): Article 17, 24 pages, DOI 10.1145/1391289.1391291.
• Reingold, O.; Trevisan, L. & Vadhan, S. (2006), "Pseudorandom walks on regular digraphs and the RL vs. L problem", Proc. 38th ACM Symposium on Theory of Computing (STOC), pp. 457–466, DOI 10.1145/1132516.1132583.