Korkeus (geometria)

Korkeus on geometriassa korkeusjanan pituus pisteen ja toisen janan välillä siten, että korkeusjana on kohtisuorassa toista, usein kannaksi kutsuttua, janaa, tai sen jatketta, vastaan. Tällöin sanotaan, että korkeus(jana) on kannan normaali(jana), ja päinvastoin.^[1] Janojen kohtaamispistettä kutsutaan kantapisteeksi.^[2]

Korkeusjanan monikulmion sivuja suurempi merkitys perustunee pinta-alojen ja tilavuuksien tunnettuihin laskukaavoihin, joissa korkeuden tunteminen on tärkeää. Korkeus on ilmeisesti tärkeä myös siksi, että ihmisen rakentaminen suuntautuu painovoimaa vastaan ja rakenteet ovat pystysuorassa eli kohtisuorassa vaakasuoraa alustaa vastaan.^[3][4][5]

Monikulmion pinta-alan määritys voidaan tehdä käyttämällä pelkästään sivujen pituuksia, sekä pituuksia ja kulmia tai sitten sivun pituuksia ja korkeutta.^[6] Seuraavassa joitakin tilanteita, joissa korkeuksia käytetään ja miten korkeus näissä tilanteissa on määritelty.

• 
  Kolmion korkeus on tylppäkulmaisella kolmiolla kärjen E etäisyys kannan jatkeelle CD. Pinta-ala lasketaan kertomalla puolikas kolmion sivun pituudella a = BC sitä vastaavalla korkeudella h: ${\displaystyle A={\tfrac {1}{2}}ah}$ ^[6]
• 
  Suunnikkaan pinta-ala voidaan laskea kertomalla sivun pituus a = HI korkeudella h = v = LK, joka on sivun HI ja sen yhdensuuntaisen vastasivun JK välinen etäisyys: ${\displaystyle A=ah}$.^[6]
• 
  Puolisuunnikkaan pinta-ala voidaan laskea kertomalla yhdensuuntaisten sivujen a = DE ja b = FG välinen etäisyys eli korkeus h = GP sivujen a ja b pituuksien keskiarvolla: ${\displaystyle A={\tfrac {a+b}{2}}h}$.^[7]

• 
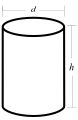  Lieriön tilavuus lasketaan kertomalla ympyrämuotoisen pohjan pinta-ala A_p lieriön korkeudella h: ${\displaystyle V=A_{p}h}$
• 
  Kartion, jollainen on myös kuvan suora neliöpohjainen pyramidi, tilavuus lasketaan kertomalla kolmasosa pohjan ABCD pinta-alan A_p ja korkeuden h = v_t tulolla: ${\displaystyle V={\tfrac {1}{3}}A_{p}h}$
• 
  Vaikka kartio olisi vino, mitataan korkeus h = v_t aina etäisyytenä pyramidin kärjestä sen pohjan tasolle mitattuna.
• 
  Katkaistun kartion tilavuus lasketaan eri kokoisten pohjan pinta-alojen ja niiden välisen etäisyyden avulla. Korkeus määritetään ylä- ja alapohjan välisenä kohtisuorana etäisyytenä h.

Kolmiolla on kolme eri korkeusjanaa, jotka kulkevat kolmion kärjen ja kantapisteen välissä. Teräväkulmaisella kolmiolla kantapiste sijaitsee aina kolmion sivulla eli kannalla, mutta tylppäkulmaisella kolmiolla jotkin kantapisteet saattavat sijaita sivun eli kannan jatkeella.

• 
  Teräväkulmaisella kolmiolla korkeusjanojen kantapisteet sijaitsevat kolmion sivuilla.
• 
  Teräväkulmaisella kolmiolla korkeusjanojen leikkauspiste, ortokeskus, voi sijaita aivan kolmion reunalla.
• 
  Suorakulmaisella kolmiolla kaksi sivua eli kateetit ovat samalla korkeusjanoja ja ortokeskus sijaitsee kolmion siinä kärjessä, jonka kulma on suora.
• 
  Tylppäkulmaisen kolmion korkeusjanojen jatkeet leikkaavat kolmion ulkopuolella. Keskimmäistä korkeusjanaa on jatketty kärjestä ylöspäin ja kahta reunimmaista korkeusjanaa on jatkettu kannan jatkeen läpi ylöspäin.

Sivujen lisäksi myös kolmion korkeusjanat määrittelevät kolmion yksikäsitteisesti. Jos kahdella kolmiolla on yhtä pitkät korkeusjanat, ovat ne yhtenevät kolmiot.^[8]

Korkeusjanat, tai niiden jatkeet, leikkaavat aina yhdessä pisteessä, jota kutsutaan ortosentriksi tai ortokeskukseksi.^[9][10][11]

Kantapisteistä voidaan piirtää kolmio, jota kutsutaan ortokolmioksi. Ortokolmion kulmanpuolittajina ovat kolmion korkeusjanat. Ortokolmion sisälle piirretyn ympyrän keskipiste on siksi ortokeskuksessa.^[12][10][11]

Kolmion ortokeskus H, painopiste G ja kolmion ympäri piirretyn ympyrän keskipiste O ovat kollineaariset eli sijaitsevat samalla suoralla. Pisteiden välisille etäisyyksille pätee HG = 2·GO.^[9][13]

Kolmion pinta-ala voidaan kolmion korkeusjanojen avulla laskea kolmella eri tavalla

${\displaystyle A={\tfrac {1}{2}}ah_{a}={\tfrac {1}{2}}bh_{b}={\tfrac {1}{2}}ch_{c}.}$ ^[14][15]

Kun R on kolmion ympäri piirretyn ympyrän säde, ja kun ${\displaystyle \beta }$ ja ${\displaystyle \gamma }$ ovat sivujen b ja c vastaiset kulmat, määräytyy kolmiossa sivua a vastaan olevan korkeusjanan ${\displaystyle h_{a}}$ pituus lausekkeista

${\displaystyle h_{a}={\frac {bc}{2R}}={\frac {2A}{a}}=c\sin \gamma =b\sin \beta .}$ ^[16]

Tasakylkisessä kolmiossa kylkien pituudet ovat b ja kanta a, jolloin kolmion korkeudet ovat

${\displaystyle h_{a}={\sqrt {b^{2}-{\tfrac {1}{4}}a^{2}}}}$ ^[17]

ja

${\displaystyle h_{b}={\frac {2A}{b}}={\frac {a{\sqrt {b^{2}-{\tfrac {1}{4}}a^{2}}}}{b}}.}$

Tasasivuisessa kolmiossa sivujen pituudet ovat a, jolloin korkeus on aina

${\displaystyle h={\frac {a{\sqrt {3}}}{2}}.}$

• Korkeus

• Seppänen, Raimo et al.: MAOL. (lukion taulukkokirja, keltainen). Helsinki: Otava, 2005. ISBN 978-951-1-20607-1.
• Seppänen, Raimo et al.: MAOL. (lukion taulukkokirja, vihreä). Helsinki: Otava, 1999. ISBN 951-1-16053-2.
• Alatupa, Sami et al.: Pitkä Sigma 3. (lukion pitkän matematiikan oppikirja). Helsinki: Otava, 2008. ISBN 978-951-26-5927-2.
• Väisälä Kalle: Geometria. Porvoo: Wsoy, 1959. Teoksen verkkoversio (pdf).
• Kurittu Lassi: Geometria (pdf) (luentomoniste) 2006. Jyväskylän: Jyväskylän Yliopisto.
• Harju, Tero: Geometrian lyhyt kurssi (pdf) (luentomoniste) users.utu.fi. 2012. Turun yliopisto. Arkistoitu 28.9.2013. Viitattu 14.12.2012.