Brocardin pisteet

Brocardin pisteet liittyvät geometriassa kolmioihin. On osoitettu, että jokaisessa kolmiossa voidaan piirtää kolmion kärjistä ceviaanit, jotka leikkaavat toisensa yhteisessä pisteessä ja samalla erkanevat samankätisestä sivusta saman suuruisen Brocardin kulman ${\displaystyle \omega }$ verran. Kulman ${\displaystyle \omega }$ suuruus riippuu kolmion kulmista. Jos ceviaanit erkanevat kulman oikeasta vai vasemmasta kyljestä, kutsutaan leikkauspisteitä vastaavasti Ensimmäiseksi- (merkitään ${\displaystyle \Omega }$) tai Toiseksi Brocardin pisteeksi (merkitään ${\displaystyle \Omega '}$). Brocardin pisteet ovat kolmion sisäpisteitä, mutta ne eivät kuulu kolmion merkillisiin pisteisiin niin sanotun symmetrian puutteen vuoksi.^[1]. Pisteet on nimetty ranskalaisen matemaatikon Henri Brocardin (1845−1922) mukaan.^[2][3][4]

Kolmion ABC sivut merkitään a, b ja c. On olemassa täsmälleen yksi piste ${\displaystyle \Omega }$, jolle janat ${\displaystyle A\Omega }$, ${\displaystyle B\Omega }$ ja ${\displaystyle C\Omega }$ muodostavat saman kulman ${\displaystyle \omega }$, sivujen c, a ja b kanssa, eli

${\displaystyle \angle \Omega AB=\angle \Omega BC=\angle \Omega CA=\omega .\,}$

Ceviaanin ja kolmion sivun välinen kulma voidaan valita kahdella tavalla. Kun käytetään ceviaanin ja kulman oikean kyljen välistä kulmaa (katso animaatiota), saadaan leikkauspisteeksi ensimmäinen Brocardin piste ja kun käytetään kulmassa vasenta kylkeä saadaan toinen Brocardin piste. Ne ovat toistensa isogonaalisia konjugaatteja.^[2][3]

Brocardin kulma ensimmäiselle- ja toiselle Brocardin pisteelle ovat aina samat. Kulman suuruus riippuu kolmion muodosta, mutta se on sellainen, että Brocardin pisteet ovat kolmion sisäpiste.^[3]

Jos kolmion kulmat ovat ${\displaystyle \alpha ,\beta }$ ja ${\displaystyle \gamma }$, saadaan Brocardin kulmaksi ${\displaystyle \omega }$

${\displaystyle \cot \omega =\cot \alpha +\cot \beta +\cot \gamma }$ ^[3]

tai jos kolmion sivut ovat ${\displaystyle a,b}$ ja ${\displaystyle c}$ sekä kolmion pinta-ala ${\displaystyle A}$, saadaan

${\displaystyle \cot \omega ={\frac {a^{2}+b^{2}+c^{2}}{4A}}.}$ ^[3]

Ensimmäinen Brocardin piste (merkitään usein ${\displaystyle \Omega }$, joskus myös ${\displaystyle \tau _{1}}$ tai ${\displaystyle Z_{1}}$) muodostuu ceviaaneista, joiden Brocardin kulma mitataan kolmion kulman oikeasta kyljestä. Pisteen trilineaariset koordinaatit ovat

${\displaystyle {\frac {c}{b}}:{\frac {a}{c}}:{\frac {b}{a}}}$.^[5]

Toisen Brocardin pisteen (merkitään ${\displaystyle \Omega '}$, joskus myös ${\displaystyle \tau _{2}}$ tai ${\displaystyle Z_{2}}$) kulma mitataan kolmion kulmien oikeasta kyljestä. Toisen pisteen trilineaariset koordinaatit ovat

${\displaystyle {\frac {b}{c}}:{\frac {c}{a}}:{\frac {a}{b}}}$.^[6]

Brocardin keskipiste (merkitään joskus ${\displaystyle M}$) sijaitsee ensimmäisen- ja toisen Brocardin pisteen yhdistävän janan keskipisteessä. Toisin kuin kaksi ensimmäistä Brocardin pistettä, Brocardin keskipiste on kolmion merkillinen piste ja tunnetaan Kimberlingin merkinnällä ${\displaystyle X_{39}}$.^[7][8]

Keskipisteen trilineaariset koordinaatit ovat

${\displaystyle a(b^{2}+c^{2}):b(c^{2}+a^{2}):c(b^{2}+c^{2})=\sin(\alpha +\omega ):\sin(\beta +\omega ):\sin(\gamma +\omega ),}$

missä ${\displaystyle \omega }$ on Brocardin kulma. Pisteen barysentriset koordinaatit ovat

${\displaystyle a^{2}(b^{2}+c^{2}):b^{2}(c^{2}+a^{2}):c^{2}(b^{2}+c^{2}).}$ ^[8]

Brocardin piste sijaitsee sellaisessa kolmion sisäpisteessä, että sen pisteen ja kolmion sivujen päätepisteiden kautta kulkevat ympyrät sivuavat kukin aina yhtä sivua tangenttiaalisesti. Kehäkulmalauseella voidaan osoittaa, että kaarta vastaan oleva kehäkulma on yhtä suuri kuin kaaren päätepisteessä olevan tangentin ja kaaren jänteen välinen kulma. Piirtämiseen tarvitaan suora kulma ja harppi.

Ensimmäisen Brocardin pisteen konstruointi aloitetaan valitsemalla kolmion sivu, johon piirretään kaksi normaalia. Sivun vasempaan päätepisteeseen on määritelty Brocardin kulma, joten piirrettävän ympyrän tangentiaalinen piste sijaitsee sivun oikeassa päätepisteeseessä. Siihen piirretään normaali, joka on kohtisuorassa viereiseen sivuun nähden. Sivulle piirretään myös keskinormaali, joka leikaa ensimmäistä normaalia. Harpilla piirretään ympyrä, joka kulkee sivun päätepisteiden kautta. Muille sivuille muodostetaan omat ympyrät samalla tavalla. Ympyrät leikkaavat yhteisessä pisteessä, joka on ensimmäinen Brocardin piste.^[4]

Toinen Brocardin toinen piste sijaitsee kolmen ympyrän leikkauspisteessä, joka muodostetaan peilikuvamaisesti. Ympyrät sivuavat tangentiaalisesti viereistä sivua nyt sivun vasemmassa päätepisteessä, koska Brocardin kulma on sivun toisessa päässä.^[4]

• 
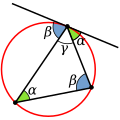  Kehäkulma ${\displaystyle \alpha }$ (vihreä) on yhtä suuri kuin jänteen ja tangentin välinen kulma.
• 
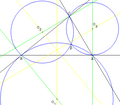  Ensimmäinen Brocardin piste
• 
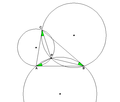  Ensimmäinen Brocardin piste
• 
  Toinen Brocardin piste

Brocardin ympyrän (engl. Brocard's circle), joka tunnetaan myös seitsemän pisteen ympyränä (engl. seven-point circle), halkaisijan muodostaa jana ${\displaystyle OK}$, jonka päätepisteitä ovat ulkoympyrän keskipiste ${\displaystyle O}$ ja symmediaaninen piste ${\displaystyle K}$.^[9]

Halkaisijan keskipiste on samalla Brocardin ympyrän keskipiste (Kimberlingin merkillinen piste ${\displaystyle X_{182}}$). Ympyrän säde voidaan laskea usealla tavalla. Kun merkitään kolmion sivut ja kolmion ympäröivän ympyrän säde sekä Brocardin kulma kirjaimilla ${\displaystyle a,b,c,R}$ ja ${\displaystyle \omega }$, saadaan säteelle lausekkeet

${\displaystyle R_{B}=R{\sqrt {(a^{4}+b^{4}+c^{4})-(a^{2}b^{2}+b^{2}c^{2}+c^{2}a^{2})}}={\frac {R{\sqrt {1-4\sin ^{2}\omega }}}{2\cos \omega }}.}$ ^[10]

Ympyrän kehällä olevia pisteitä ovat ainakin

• molemmat Brocardin pisteet ${\displaystyle \Omega }$ ja ${\displaystyle \Omega '}$, jotka sijaitsevat Brocardin janan suhteen symmetrisesti
• Kolmion keskinormaalien leikkauspiste ${\displaystyle O}$ eli ${\displaystyle X_{3}}$
• symmediaaninen piste ${\displaystyle K}$ eli ${\displaystyle X_{6}}$
• kaksi muuta merkillistä pistettä (Kimberlingin merkintä ${\displaystyle X_{1083}}$ ja ${\displaystyle X_{1316}}$)
• nimensä mukaan vielä yksi tunnettu merkillinen piste.

• 
  Brocardin ympyrä. Sy merkitsee symmediaanista pistettä ja Cc keskinormaalien leikkauspiste.

Ensimmäinen Brocardin kolmio syntyy Brocardin ympyrään siten, että ceviaanit, jotka kulkevat ensimmäisen Brocardin pisteen kautta, leikkaavat ympyrän kolmessa pisteessä. Ceviaanit, jotka kulkevat toisen Brocardin pisteen kautta, leikkaavat saman ympyrän samoissa pisteissä. Kolmio syntyy, kun nämä kolme pistettä yhdistetään janoilla, ja se on käänteisesti yhdenmuotoinen referenssikolmion kanssa. Käänteisesti yhdenmuotoiset monikulmioiden kulmat ovat samat, mutta esiintyvät käänteisessä järjestyksessä.^[11]

Kun referenssikolmion kärjistä piirtää sitä ympäröivälle ympyrälle suorat, jotka ovat ensimmäisen Brocardin kolmion sivujen suuntaisia, leikkaavat ne ympyrän kehällä yhteisessä pisteessä. Pistettä kutsutaan Steinerin pisteeksi ja se on eräs kolmion merkillinen piste (Kimberlingin merkinnöin ${\displaystyle X_{99}}$).^[12][13]

Koska Brocardin kolmio on yhdenmuotoinen referenssikolmionsa kanssa, voidaan sivujen pituudet ja pinta-ala laskea ketoimen ${\displaystyle \sigma }$ avulla:

${\displaystyle a'=\sigma a}$

${\displaystyle b'=\sigma b}$ ja

${\displaystyle c'=\sigma c}$

sekä

${\displaystyle A'=\sigma ^{2}A,}$

missä

${\displaystyle \sigma ={\frac {\sqrt {a^{4}-a^{2}b^{2}+b^{4}-a^{2}c^{2}-b^{2}c^{2}+c^{4}}}{a^{2}+b^{2}+c^{2}}}.}$ ^[14]

Referenssikolmion painopiste (Kimberlingin merkinnöin ${\displaystyle X_{2}}$) on yhteinen Brocardin kolmion painopisteen kanssa ja symmediaaninen piste on Brocardin kolmion Steinerin piste.^[14]

Toinen Brocardin kolmio syntyy kuuden ympyrän kaarista, jotka kulkevat sivun päätepisteiden ja toisen Brocardin pisteen kautta. Samasta kolmion kärjestä erkanevat ja eri Brocardin pisteen kautta kulkevat ympyrät leikkaavat toisensa yhdessä toisen Brocardin kolmion kärjessä. Toinen tapa konstruoida tämä kolmio on piirtää ceviaanit symmediaaniseen pisteeseen, jolloin ceviaanien ja Brocardin ympyrän leikkauspisteet muodostavat toisen Brocardin kolmion kärjet. Tämä kolmio ei ole yhdenmuotoinen referenssikolmion kanssa. Sen keskinormaalien leikkauspiste ${\displaystyle X_{3}}$ on referenssikolmion Brocardin ympyrän keskipiste ${\displaystyle X_{182}}$.^[15]

Jos referenssikolmiolle piirtää ulkoympyrän ja jatkaa symmediaaniselle pisteelle ${\displaystyle K}$ piirrettyjä ceviaaneja ulkoympyrälle saakka, sijaitsevat toisen Brocardin kolmion kärjet näiden jatkettujen ceviaanien keskipisteissä.^[15]

On olemassa myös kolmas- ja neljäs Brocardin kolmio.^[16]

• Kimberling; Clark: Central Points and Central Lines in a Plane of a Triangle, Mathematical Magazine, vol 67, issue 3, s. 163–187, myös täällä^{[vanhentunut linkki]}.
• Kimberling; Clark: Triangle Centers as Functions, Rocky Mountain Journal of Mathematics, 23/1993, (s.1269–1286)
• De punten van Brocard
• Pamfilos, Paris: Brocard points, Brocard angle, Kreetan yliopisto
• Pamfilos, Paris: Second Brocard Triangle, Kreetan yliopisto
• Pamfilos, Paris: Brocard ellipse, Kreetan yliopisto
• Pamfilos, Paris: Median triangle, Kreetan yliopisto
• Pamfilos, Paris: Rotating triangle's sides about their middle, Kreetan yliopisto
• Pamfilos, Paris: Yagci's problem, Kreetan yliopisto