Kiepert conics

In triangle geometry, the Kiepert conics are two special conics associated with the reference triangle. One of them is a hyperbola, called the Kiepert hyperbola and the other is a parabola, called the Kiepert parabola. The Kiepert conics are defined as follows:

If the three triangles ${\displaystyle A^{\prime }BC}$, ${\displaystyle AB^{\prime }C}$ and ${\displaystyle ABC^{\prime }}$, constructed on the sides of a triangle ${\displaystyle ABC}$ as bases, are similar, isosceles and similarly situated, then the triangles ${\displaystyle ABC}$ and ${\displaystyle A^{\prime }B^{\prime }C^{\prime }}$ are in perspective. As the base angle of the isosceles triangles varies between ${\displaystyle -\pi /2}$ and ${\displaystyle \pi /2}$, the locus of the center of perspectivity of the triangles ${\displaystyle ABC}$ and ${\displaystyle A^{\prime }B^{\prime }C^{\prime }}$ is a hyperbola called the Kiepert hyperbola and the envelope of their axis of perspectivity is a parabola called the Kiepert parabola.

It has been proved that the Kiepert hyperbola is the hyperbola passing through the vertices, the centroid and the orthocenter of the reference triangle and the Kiepert parabola is the parabola inscribed in the reference triangle having the Euler line as directrix and the triangle center X₁₁₀ as focus.^[1] The following quote from a paper by R. H. Eddy and R. Fritsch is enough testimony to establish the importance of the Kiepert conics in the study of triangle geometry:^[2]

"If a visitor from Mars desired to learn the geometry of the triangle but could stay in the earth's relatively dense atmosphere only long enough for a single lesson, earthling mathematicians would, no doubt, be hard-pressed to meet this request. In this paper, we believe that we have an optimum solution to the problem. The Kiepert conics ...."

The Kiepert hyperbola was discovered by Ludvig Kiepert while investigating the solution of the following problem proposed by Emile Lemoine in 1868: "Construct a triangle, given the peaks of the equilateral triangles constructed on the sides." A solution to the problem was published by Ludvig Kiepert in 1869 and the solution contained a remark which effectively stated the locus definition of the Kiepert hyperbola alluded to earlier.^[2]

Let ${\displaystyle a,b,c}$ be the side lengths and ${\displaystyle A,B,C}$ the vertex angles of the reference triangle ${\displaystyle ABC}$.

The equation of the Kiepert hyperbola in barycentric coordinates ${\displaystyle x:y:z}$ is

${\displaystyle {\frac {b^{2}-c^{2}}{x}}+{\frac {c^{2}-a^{2}}{y}}+{\frac {a^{2}-b^{2}}{z}}=0.}$

• The centre of the Kiepert hyperbola is the triangle center X(115). The barycentric coordinates of the center are

${\displaystyle (b^{2}-c^{2})^{2}:(c^{2}-a^{2})^{2}:(a^{2}-b^{2})^{2}}$.

• The asymptotes of the Kiepert hyperbola are the Simson lines of the intersections of the Brocard axis with the circumcircle.
• The Kiepert hyperbola is a rectangular hyperbola and hence its eccentricity is ${\displaystyle {\sqrt {2}}}$.

1. The center of the Kiepert hyperbola lies on the nine-point circle. The center is the midpoint of the line segment joining the isogonic centers of triangle ${\displaystyle ABC}$ which are the triangle centers X(13) and X(14) in the Encyclopedia of Triangle Centers.
2. The image of the Kiepert hyperbola under the isogonal transformation is the Brocard axis of triangle ${\displaystyle ABC}$ which is the line joining the symmedian point and the circumcenter.
3. Let ${\displaystyle P}$ be a point in the plane of a nonequilateral triangle ${\displaystyle ABC}$ and let ${\displaystyle p}$ be the trilinear polar of ${\displaystyle P}$ with respect to ${\displaystyle ABC}$. The locus of the points ${\displaystyle P}$ such that ${\displaystyle p}$ is perpendicular to the Euler line of ${\displaystyle ABC}$ is the Kiepert hyperbola.

The Kiepert parabola was first studied in 1888 by a German mathematics teacher Augustus Artzt in a "school program".^[2][3]

• The equation of the Kiepert parabola in barycentric coordinates ${\displaystyle x:y:z}$ is

${\displaystyle f^{2}x^{2}+g^{2}y^{2}+h^{2}z^{2}-2fgxy-2ghyz-2hfzx=0}$
where
${\displaystyle f=(b^{2}-c^{2})/a,g=(c^{2}-a^{2})/b,h=(a^{2}-b^{2})/c}$.

• The focus of the Kiepert parabola is the triangle center X(110). The barycentric coordinates of the focus are

${\displaystyle a^{2}/(b^{2}-c^{2}):b^{2}/(c^{2}-a^{2}):c^{2}/(a^{2}-b^{2})}$

• The directrix of the Kiepert parabola is the Euler line of triangle ${\displaystyle ABC}$.

• 
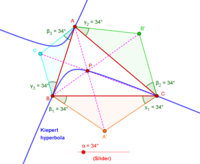  Kiepert hyperbola showing the center of perspectivity of triangles ABC and A'B'C'
• 
  Kiepert hyperbola showing the orthocenter, the incenter and the perpendicular asymptotes
• 
  Kiepert parabola of triangle ABC. The figure also shows a member (line LMN) of the family of lines whose envelope is the Kiepert parabola.
• 
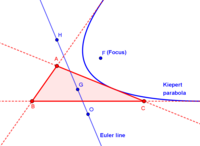  Kiepert parabola showing the focus and the directrix

• Triangle conic
• Modern triangle geometry

• Weisstein, Eric W. "Kiepert Hyperbola". MathWorld--A Wolfram Web Resource. Retrieved 5 February 2022.
• Weisstein, Eric W. "Kiepert Parabola". MathWorld--A Wolfram Web Resource. Retrieved 5 February 2022.